Clustering – Partitioning Methods定义Partitioning method形心 centroid of a clusterK-mean符号规定算法分析k-MedianSilhouette-CoefficientEvaluatingReference
划分方法是一种聚类算法,可以用来为大数据洞察数据的分布,做自动归类等作用。
定义
Partitioning method
给定一个
也就是说,划分方法把数据划分成了
划分方法的一个准则是(或者判断一个划分是否是一个好的划分的标准是):同一个簇中的对象尽可能相关,不同簇的对象尽可能无关。
基于划分的聚类可能是效率低下的,因为遍历所有的项通常很慢。可以使用启发式算法来提升效率。
目前流行的启发式算法过程如下:
给每个簇挑选
递归地改善刚刚挑选到的簇:
- 在当前的聚类(clustering)下,把每个对象分配到最合适的簇(cluster)中
- 基于刚才的重新聚类,重新计算新的簇的代表。
- 重复到不再改变
启发式算法会渐近地提高聚类的质量,进而逼近局部最优解。本小节介绍的k-mean算法就是一种启发式算法。
数学的定义如下:
Given a set
-
i.e. each element of
形心 centroid of a cluster
形心是一个簇的中心点。
形心点有多种形式可以定义,可以用一个簇的所有值的均值或者是一个簇的中心点。
K-mean
K-mean 算法的目的是:
Find a clustering such that the within-cluster variation of each cluster is small and use the centroid of a cluster as a representative.
找到一个聚类(clustering),使得每个簇的簇内变差是很小的,并且使用形心作为代表.[1] 簇内变差的定义见下文中的符号规定。
符号规定
对象(objects)
平方距离和(用来衡量一个簇的紧凑程度(compactness))(sum of squared distances):
其中
对于整个聚类
也就是整个数据集
有的书上也用簇内变差
其中
最佳划分:
算法
目前已经证明,即使是数据的维度只有二维,簇的数量不固定,想要找到最佳划分使得
但是如果簇和数据的维度都给定,那么问题可以在
k-mean算法则是利用贪心算法,将复杂度尽可能的降低。算法首先在数据集中随机选择
具体过程如下:
输入:
- 给定
- 给定包含
初始化:
- 挑选k个随机代表对象
重复:
- 把
- 为每个簇重新计算形心,并把每个形心作为新的代表对象
直到:
- 代表对象不再改变
分析
k-mean算法复杂度是
优势:
- 算法复杂度通常情况下比较低
- 易于部署。
局限性在于:
- 必须给出簇的均值的定义。
- 要求用户事前给出
- 对噪声和离群点敏感。因为少量的极值会对均值产生很大影响。
- 簇要求形状得是凸的
- 性能或者说是时间复杂度与初始化的关系很大。
k-Median
k-mean算法对离群点比较敏感。改进的一种想法是不让对象和均值比较,而是让对象和对象比较。
具体来说,我们为每一个簇挑选一个代表对象。然后让剩下的对象和这些代表对象比,找到与代表对象最相似的,将对象放入代表对象所对应的簇中。
与
其中
当k=1时,找中心点的时间复杂度是
k-median算法同样可以计算无法取均值的ordering数据。
k-median算法与k-mean类似,只是公式不同,在此不做赘述,有兴趣可以阅读这篇文章,介绍了k-mean,k-median,以及衍生出的PAM。
Silhouette-Coefficient
如何挑选参数k呢?非常简单的想法是遍历k的大小,从2一直到n-1,n是数据的规模。然后我们挑选出最好的聚类所对应的k。
那么我们应该如何衡量一个好的聚类呢?单纯只是用
Silhouette-Coefficient可以评估一个聚类的质量。挑选它的原因也很简单,这个系数不会因为k的增加而单调。
Silhouette-Coefficient的想法是,聚类的质量好坏,对应于这个聚类是否将对象“恰当”得映射到了聚类里。所谓恰当,正如我们前面提到的,就是想让同一个簇内的对象尽可能相似,不同的簇的对象尽可能相异。那么我们就可以规定
有了这个想法,
可以用下面的图片来表示上面的定义。
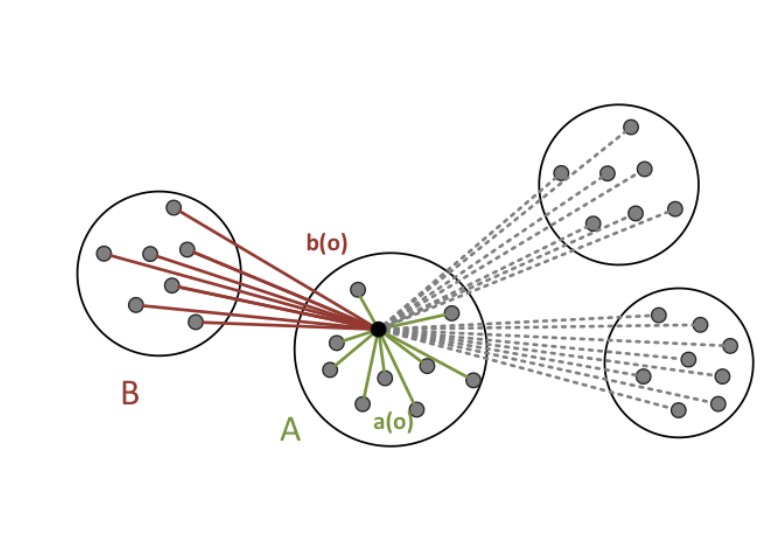
Silhouette Coefficient定义如下:
可以看出
通过silhouette coefficient, 我们定义一个簇
一个聚类
Evaluating
对于一个簇来说,
如果
对于一个聚类来说,
如果
Reference
[1] S.P. Lloyd: Least squares quantization in PCM. In IEEE Information Theory, 1982

又是一个我插不上嘴的博客,太专业了
谢谢回复!
这里写的也只是一些皮毛罢了。
你的导航站也很棒啊,很开心能遇到这么多2022依然在坚持用博客的人:)